Introdução: O Desafio da Caixa Preta em Machine Learning
O Paradoxo da Complexidade
À medida que modelos de Machine Learning se tornam mais sofisticados e pervasivos em ambientes corporativos, emerge um paradoxo fundamental: quanto mais complexo e preciso o modelo, menos transparente ele se torna. Este fenômeno, conhecido como o “paradoxo da caixa preta”, apresenta desafios significativos para organizações que necessitam não apenas de previsões precisas, mas também de justificativas claras para suas decisões automatizadas.
Em um cenário onde decisões algorítmicas impactam diretamente stakeholders e processos críticos de negócio, a necessidade de explicabilidade transcende a mera preferência técnica — torna-se um imperativo estratégico e, frequentemente, regulatório.
A Necessidade de Explicabilidade
A explicabilidade em Machine Learning vai além da simples transparência do modelo. Ela representa a capacidade de fornecer justificativas claras e compreensíveis para as decisões algorítmicas, permitindo que stakeholders compreendam o racional por trás das previsões, identifiquem potenciais vieses, validem a conformidade com requisitos regulatórios e construam confiança nos sistemas automatizados.
Taxonomia da Interpretabilidade em ML
A interpretabilidade em Machine Learning pode ser categorizada em diferentes abordagens, cada uma com suas características e aplicações específicas. Esta taxonomia nos ajuda a entender as opções disponíveis e escolher as técnicas mais adequadas para cada contexto.
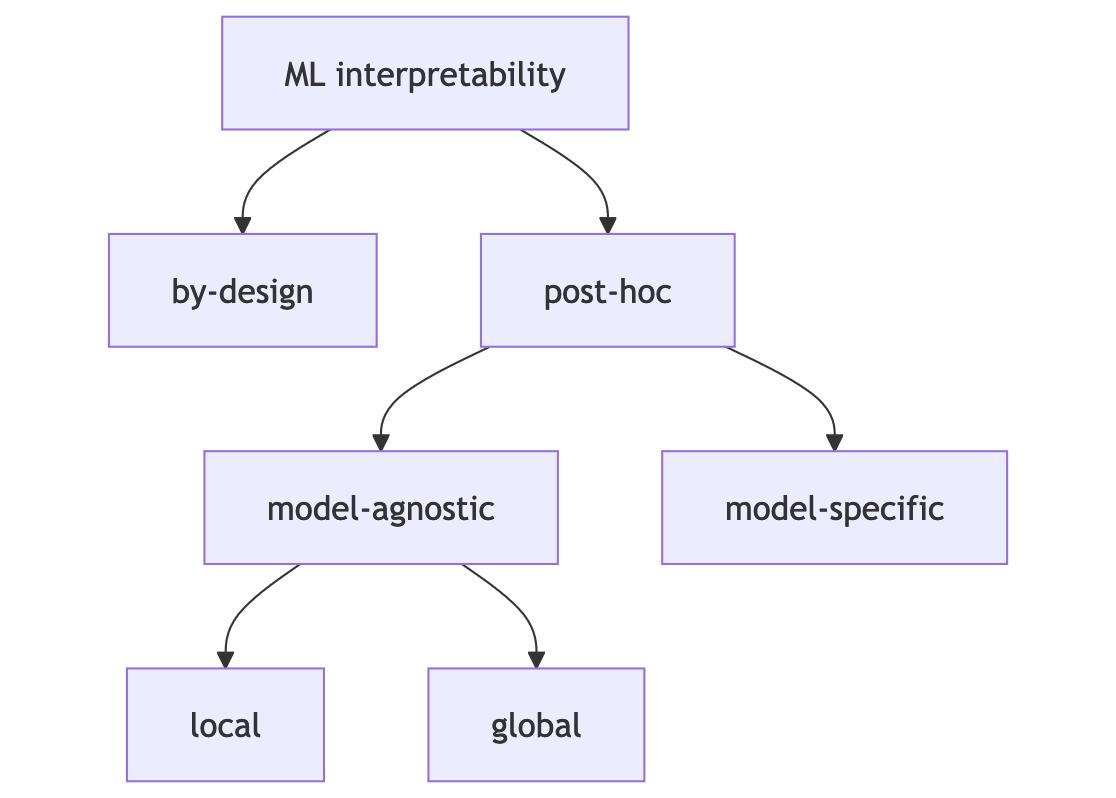 Figura: Taxonomia das diferentes abordagens de interpretabilidade em Machine Learning.
Figura: Taxonomia das diferentes abordagens de interpretabilidade em Machine Learning.
By-Design (Interpretabilidade Intrínseca) Modelos naturalmente interpretáveis (ex: árvores de decisão, regressão linear) oferecem transparência nas decisões desde sua concepção, embora possam apresentar compromisso potencial com a performance.
Post-Hoc (Interpretabilidade Posterior) Esta abordagem realiza a análise após o treinamento do modelo e divide-se em duas categorias principais:
Model-Agnostic (Agnóstico ao Modelo) Funciona com qualquer tipo de modelo, sendo LIME e SHAP exemplos populares. Permite análise tanto local (explicações individuais) quanto global (comportamento geral).
Model-Specific (Específico ao Modelo) Utiliza técnicas específicas para certos tipos de modelos, como a visualização de camadas em redes neurais.
Em nosso estudo, focaremos principalmente em técnicas post-hoc model-agnostic, que oferecem maior flexibilidade e aplicabilidade.
O Caso de Estudo: Adult Census Income Dataset
Contextualização do Problema
O Adult Census Income Dataset representa um microcosmo das decisões automatizadas que organizações enfrentam diariamente. Extraído do censo dos EUA de 1994, este dataset encapsula o desafio de prever renda individual com base em características demográficas e profissionais — uma tarefa aparentemente direta, mas repleta de nuances críticas para aplicações corporativas.
Descrição do Dataset O conjunto de dados compreende 48.842 registros com 14 atributos, incluindo variáveis demográficas, indicadores educacionais e profissionais, características de emprego e carga horária, e uma variável alvo binária: renda anual acima ou abaixo de $50.000.
Relevância para Cenários Corporativos Este dataset espelha desafios reais em diversos contextos organizacionais, desde serviços financeiros até recursos humanos, marketing e políticas públicas. Sua complexidade e características do mundo real o tornam ideal para demonstrar técnicas de XAI em contextos práticos.
Objetivos da Análise Nossa análise tem três objetivos principais: explorar técnicas de XAI em um problema de classificação de renda, avaliar o impacto de diferentes técnicas de explicabilidade na compreensão das decisões do modelo, e demonstrar como explicabilidade pode informar decisões estratégicas e mitigar riscos em contextos corporativos.
Desafios e Oportunidades
Características do Dataset O conjunto de dados apresenta características que o tornam particularmente adequado para explorar XAI. Possui uma mistura de variáveis numéricas e categóricas, dados do mundo real com ruído e valores ausentes típicos de cenários reais, e relações complexas com interações não-lineares entre variáveis.
Complexidades Específicas O dataset apresenta três complexidades principais que demandam atenção especial. Primeiro, o desbalanceamento de classes, com aproximadamente 75% dos indivíduos ganhando ≤$50K, exigindo técnicas específicas para lidar com o desbalanceamento e impactando a interpretabilidade das previsões. Segundo, a presença de variáveis sensíveis como raça, gênero e idade, que demandam monitoramento de viés e importância da explicabilidade para compliance. Terceiro, a necessidade de granularidade nas explicações, exigindo um balanço entre precisão técnica e clareza, com adaptação para diferentes stakeholders.
Potenciais Aplicações Práticas As aplicações práticas deste estudo se dividem em três áreas principais. Na primeira, o desenvolvimento de um framework de decisão explicável, com pipelines de ML transparentes, integração com sistemas de decisão existentes e documentação automatizada de decisões. Na segunda, o monitoramento de equidade, com detecção proativa de viés, análise de impacto em subgrupos e relatórios de conformidade regulatória. Na terceira, a otimização de processos, com identificação de fatores-chave para sucesso, refinamento de critérios de decisão e melhoria contínua baseada em feedback.
Metodologia de Análise
Framework de Interpretabilidade
Nossa metodologia segue um framework estruturado em dois níveis principais, combinando análise global e local para uma compreensão abrangente do modelo.
Nível Global: A análise global busca compreender o comportamento geral do modelo, identificando as variáveis mais importantes e analisando tendências gerais nos dados. Esta abordagem permite uma visão holística do funcionamento do sistema.
Nível Local: No nível local, focamos em explicações para previsões individuais, identificando fatores decisivos em casos específicos e analisando casos atípicos. Esta granularidade é essencial para entender decisões pontuais do modelo.
Critérios de Avaliação
Para avaliar a efetividade das técnicas de XAI, utilizamos os seguintes critérios:
Completude: Capacidade de explicar todas as decisões do modelo, com cobertura de diferentes tipos de previsões e consistência nas explicações.
Consistência: Estabilidade das explicações para previsões similares, robustez a pequenas variações nos dados e alinhamento com conhecimento de domínio.
Acessibilidade: Clareza e compreensibilidade das explicações, adaptação para diferentes públicos e utilidade prática para tomada de decisão.
Métricas Selecionadas
Para avaliar a qualidade das explicações, utilizamos métricas específicas para cada técnica de XAI. No SHAP (SHapley Additive exPlanations), analisamos valores SHAP médios por feature, interação entre pares de features e dependência parcial das features mais importantes. No LIME (Local Interpretable Model-agnostic Explanations), avaliamos a fidelidade local do modelo explicativo, estabilidade das explicações em vizinhanças e consistência entre diferentes amostras. Por fim, nos PDP/ICE (Partial Dependence Plots / Individual Conditional Expectation), examinamos curvas de dependência parcial, heterogeneidade das respostas individuais e interações entre features principais.
Pipeline Analítico
Pré-processamento Orientado à Interpretabilidade
Nossa abordagem de pré-processamento prioriza a manutenção da interpretabilidade. O tratamento de dados ausentes inclui documentação clara de estratégias de imputação, preservação de padrões originais e rastreabilidade das transformações. Na engenharia de features, criamos variáveis semanticamente significativas, mantemos relações interpretáveis e documentamos o processo de criação. Na normalização e escalonamento, preservamos distribuições originais, mantemos limites interpretáveis e garantimos rastreabilidade das transformações.
Estratégia de Modelagem
Nossa estratégia de modelagem é guiada pela necessidade de explicabilidade. Na seleção de modelos, priorizamos modelos intrinsecamente interpretáveis, usamos modelos de complexidade controlada e combinamos diferentes abordagens. Nas técnicas de XAI, empregamos SHAP (SHapley Additive exPlanations), LIME (Local Interpretable Model-agnostic Explanations), PDP (Partial Dependence Plots) e ICE (Individual Conditional Expectation). Na visualização e comunicação, utilizamos gráficos de importância de features, mapas de calor de interações e explicações narrativas estruturadas.
Métodos de Validação
Para garantir a robustez de nossas análises, implementamos três métodos principais. Na validação cruzada, avaliamos a estabilidade das explicações, verificamos consistência entre folds e analisamos sensibilidade. Nos testes de robustez, realizamos perturbação controlada dos dados, avaliação de sensibilidade a ruído e verificação de estabilidade temporal. Na validação com stakeholders, coletamos feedback de especialistas de domínio, realizamos testes de compreensibilidade e avaliamos utilidade prática.
Análise Exploratória Orientada à Interpretabilidade
A análise exploratória de dados é fundamental para compreender as características do dataset e estabelecer as bases para uma modelagem interpretável. A análise univariada examina cada variável isoladamente, revelando suas distribuições e características intrínsecas. Já a análise bivariada explora as relações entre pares de variáveis, identificando padrões e correlações que podem influenciar a interpretabilidade do modelo.
Esta abordagem dupla é essencial para identificar potenciais vieses e anomalias nos dados, compreender a distribuição das variáveis sensíveis, detectar relações que podem impactar a explicabilidade e estabelecer uma base sólida para a interpretação dos resultados. Através desta análise, podemos antecipar desafios de interpretabilidade e planejar estratégias adequadas para a explicação do modelo.
Primeiro, vamos carregar e preparar nossos dados:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from ucimlrepo import fetch_ucirepo
# Configuração para melhor visualização
plt.style.use('seaborn')
sns.set_palette("husl")
plt.rcParams['figure.figsize'] = [10, 6]
# Carregando os dados usando ucimlrepo
adult = fetch_ucirepo(id=2)
# Obtendo features e target
X = adult.data.features
y = adult.data.targets
# Combinando em um único DataFrame para análise
df = pd.concat([X, y], axis=1)
# Limpeza básica dos dados
df = df.replace(' ?', np.nan) # Substituindo '?' por NaN
# Exibindo informações sobre o dataset
print("Informações do Dataset:")
print(df.info())
print("\nPrimeiras linhas:")
print(df.head())
# Exibindo metadados do dataset
print("\nMetadados do UCI:")
print(f"Nome: {adult.metadata.name}")
print(f"Número de instâncias: {adult.metadata.num_instances}")
print(f"Número de features: {adult.metadata.num_features}")
Output
Informações do Dataset: <class 'pandas.core.frame.DataFrame'> RangeIndex: 48842 entries, 0 to 48841 Data columns (total 15 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 age 48842 non-null int64 1 workclass 47879 non-null object 2 fnlwgt 48842 non-null int64 3 education 48842 non-null object 4 education-num 48842 non-null int64 5 marital-status 48842 non-null object 6 occupation 47876 non-null object 7 relationship 48842 non-null object 8 race 48842 non-null object 9 sex 48842 non-null object 10 capital-gain 48842 non-null int64 11 capital-loss 48842 non-null int64 12 hours-per-week 48842 non-null int64 13 native-country 48568 non-null object 14 income 48842 non-null object dtypes: int64(6), object(9) memory usage: 5.6+ MB ... Metadados do UCI: Nome: Adult Número de instâncias: 48842 Número de features: 14
Análise Univariada e Bivariada
A distribuição de renda no conjunto de dados revela um desequilíbrio característico: aproximadamente 75% dos indivíduos apresentam renda inferior a $50.000, refletindo a realidade socioeconômica da época.
# Análise da distribuição de renda
plt.figure(figsize=(8, 6))
sns.countplot(data=df, x='income')
plt.title('Distribuição de Renda')
plt.xlabel('Renda > $50K')
plt.ylabel('Contagem')
# Removendo espaços e pontos finais das classes de renda para evitar duplicidade
df['income'] = df['income'].str.strip().str.replace('.', '', regex=False)
# Calculando as proporções
income_props = df['income'].value_counts(normalize=True)
print("Proporção das classes:")
print(f"<=50K: {income_props.iloc[0]:.2%}")
print(f">50K: {income_props.iloc[1]:.2%}")
Output
Proporção das classes: <=50K: 76.07% >50K: 23.93%
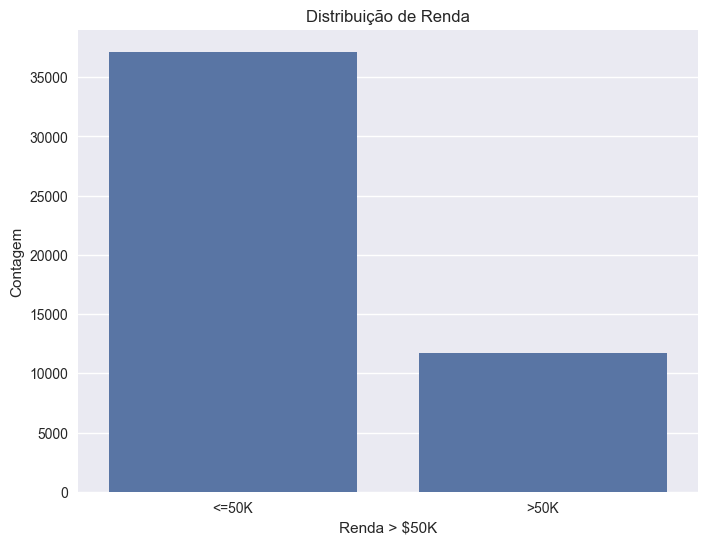 Figura: Distribuição das classes de renda no dataset após tratamento dos dados.
Figura: Distribuição das classes de renda no dataset após tratamento dos dados.
A variável idade apresenta uma concentração significativa entre 28 e 48 anos, com uma média de 38 anos. Esta distribuição tem implicações importantes para a interpretabilidade do modelo.
# Análise da distribuição de idade
plt.figure(figsize=(10, 6))
sns.histplot(data=df, x='age', hue='income', multiple="stack", bins=30)
plt.title('Distribuição de Idade por Faixa de Renda')
plt.xlabel('Idade')
plt.ylabel('Contagem')
# Estatísticas descritivas da idade
print("\nEstatísticas de Idade:")
print(df['age'].describe())
Output
Estatísticas de Idade: count 48842.000000 mean 38.643585 std 13.710510 min 17.000000 25% 28.000000 50% 37.000000 75% 48.000000 max 90.000000
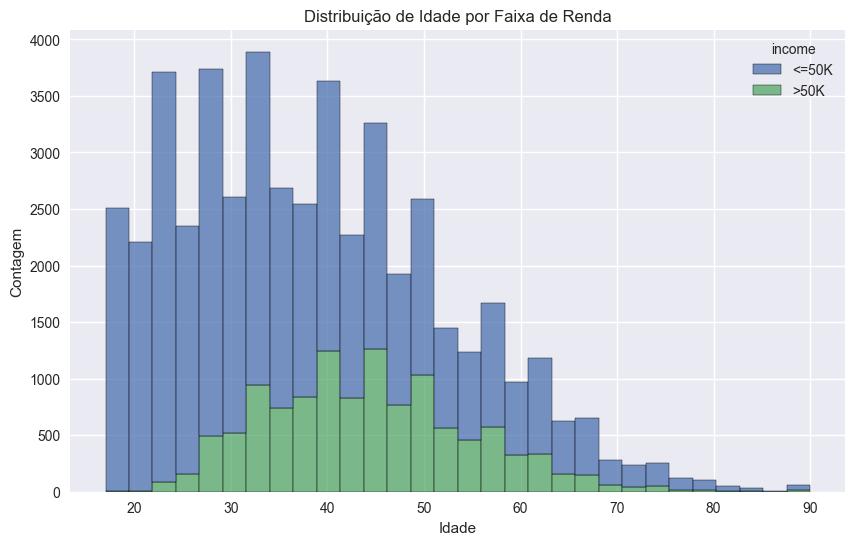 Figura: Distribuição das classes de renda ao longo das faixas etárias.
Figura: Distribuição das classes de renda ao longo das faixas etárias.
Ao analisar a relação entre educação e renda, observamos um padrão claro: níveis educacionais mais altos estão fortemente associados a rendas superiores.
# Análise da relação entre educação e renda
plt.figure(figsize=(12, 6))
education_income = pd.crosstab(df['education'], df['income'], normalize='index')
education_income.plot(kind='bar', stacked=True)
plt.title('Proporção de Renda por Nível Educacional')
plt.xlabel('Nível Educacional')
plt.ylabel('Proporção')
plt.xticks(rotation=45)
plt.tight_layout()
plt.legend(title='income', loc='upper left', bbox_to_anchor=(1,1))
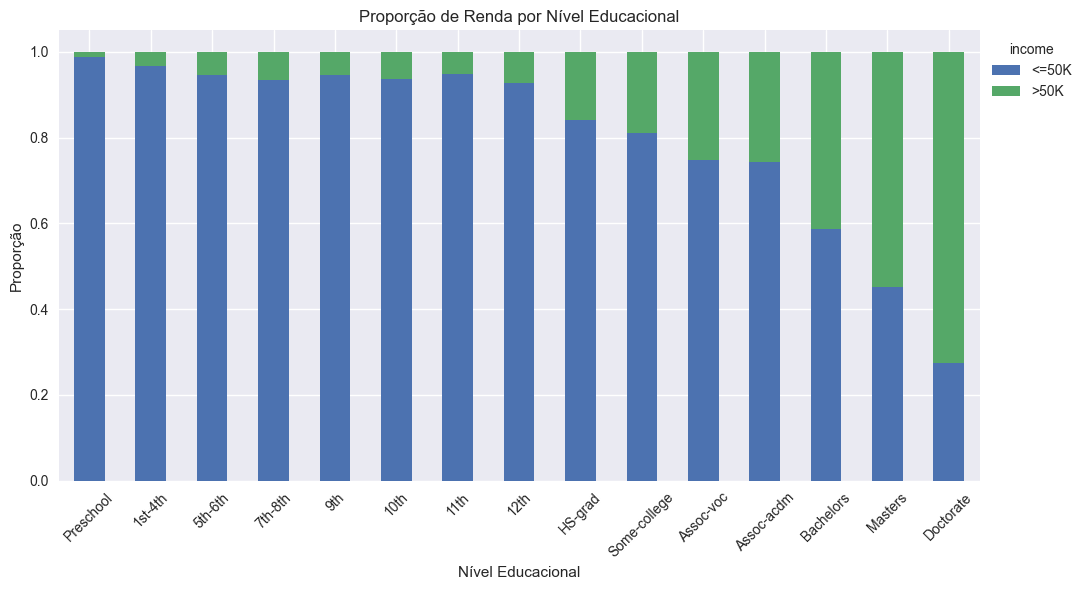 Figura: Proporção das classes de renda por nível educacional.
Figura: Proporção das classes de renda por nível educacional.
Observa-se que níveis educacionais mais altos estão fortemente associados a uma maior proporção de indivíduos com renda superior a $50K.
Análise da Relação entre Ocupação e Renda
A ocupação é um dos principais determinantes de renda e pode revelar desigualdades estruturais no mercado de trabalho. Para garantir uma análise mais precisa, valores ausentes na variável ocupação foram removidos do gráfico.
# Removendo linhas com ocupação desconhecida ('?')
removed_rows = df[df['occupation'] == '?'].shape[0]
df_occ = df[df['occupation'] != '?']
print(f"Linhas removidas: {removed_rows}")
# Análise de ocupações (sem valores ausentes e ordenando por proporção de >50K)
occupation_income = pd.crosstab(df_occ['occupation'], df_occ['income'], normalize='index')
occupation_income = occupation_income.sort_values(by='>50K', ascending=False)
plt.figure(figsize=(14, 6))
occupation_income.plot(kind='bar', stacked=True)
plt.title('Proporção de Renda por Ocupação (ordenado por >50K)')
plt.xlabel('Ocupação')
plt.ylabel('Proporção')
plt.xticks(rotation=45)
plt.tight_layout()
plt.legend(title='income', loc='upper left', bbox_to_anchor=(1,1))
Output
Linhas removidas: 1843
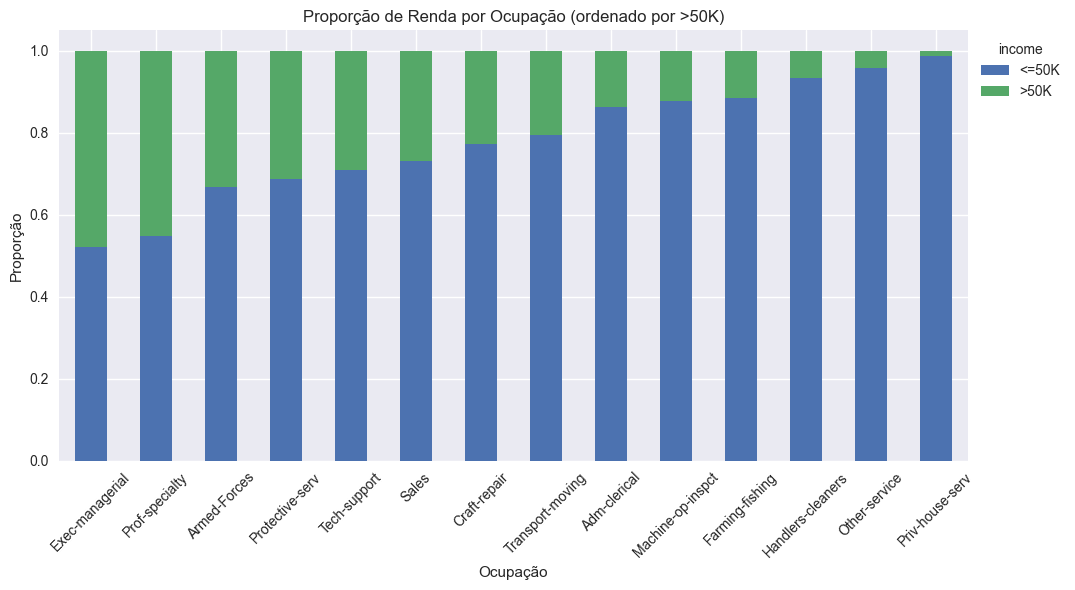 Figura: Proporção das classes de renda por ocupação (sem valores ausentes).
Figura: Proporção das classes de renda por ocupação (sem valores ausentes).
Observa-se que algumas ocupações concentram uma proporção significativamente maior de indivíduos com renda superior a $50K, enquanto outras permanecem predominantemente na faixa mais baixa, refletindo desigualdades do mercado de trabalho.
Análise de Gênero e Renda
A análise de gênero é essencial para identificar possíveis vieses e desigualdades salariais, tema central em XAI e compliance. Avaliar a distribuição de renda entre homens e mulheres permite antecipar riscos de discriminação algorítmica.
# Análise de gênero e renda
plt.figure(figsize=(6, 6))
gender_income = pd.crosstab(df['sex'], df['income'], normalize='index')
gender_income.plot(kind='bar', stacked=True)
plt.title('Proporção de Renda por Gênero')
plt.xlabel('Gênero')
plt.ylabel('Proporção')
plt.tight_layout()
plt.legend(title='income', loc='upper left', bbox_to_anchor=(1,1))
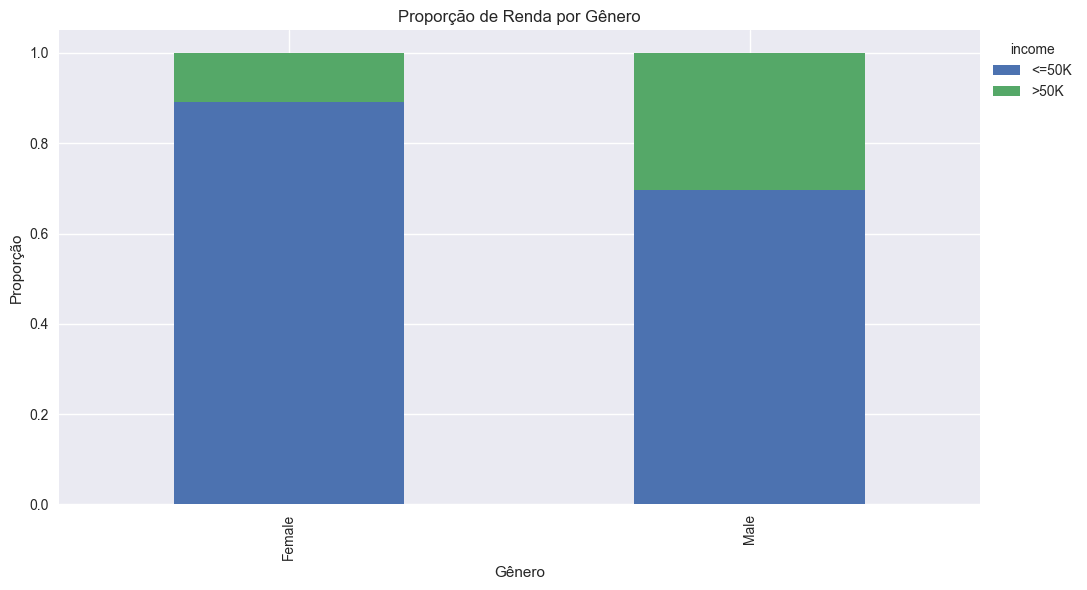 Figura: Proporção das classes de renda por gênero.
Figura: Proporção das classes de renda por gênero.
Nota-se, pelo gráfico, que a proporção de indivíduos com renda superior a $50K é consideravelmente maior entre homens do que entre mulheres. Essa diferença quantitativa destaca a importância de monitorar possíveis vieses de gênero em análises e modelos preditivos.
Análise de Raça e Renda
A variável raça é sensível e sua análise é fundamental para garantir justiça e equidade nos modelos. Avaliar a distribuição de renda por raça permite identificar possíveis disparidades e orientar ações de fairness.
# Análise de raça e renda
plt.figure(figsize=(10, 6))
race_income = pd.crosstab(df['race'], df['income'], normalize='index')
race_income = race_income.sort_values(by='>50K', ascending=False)
race_income.plot(kind='bar', stacked=True)
plt.title('Proporção de Renda por Raça (ordenado por >50K)')
plt.xlabel('Raça')
plt.ylabel('Proporção')
plt.tight_layout()
plt.legend(title='income', loc='upper left', bbox_to_anchor=(1,1))
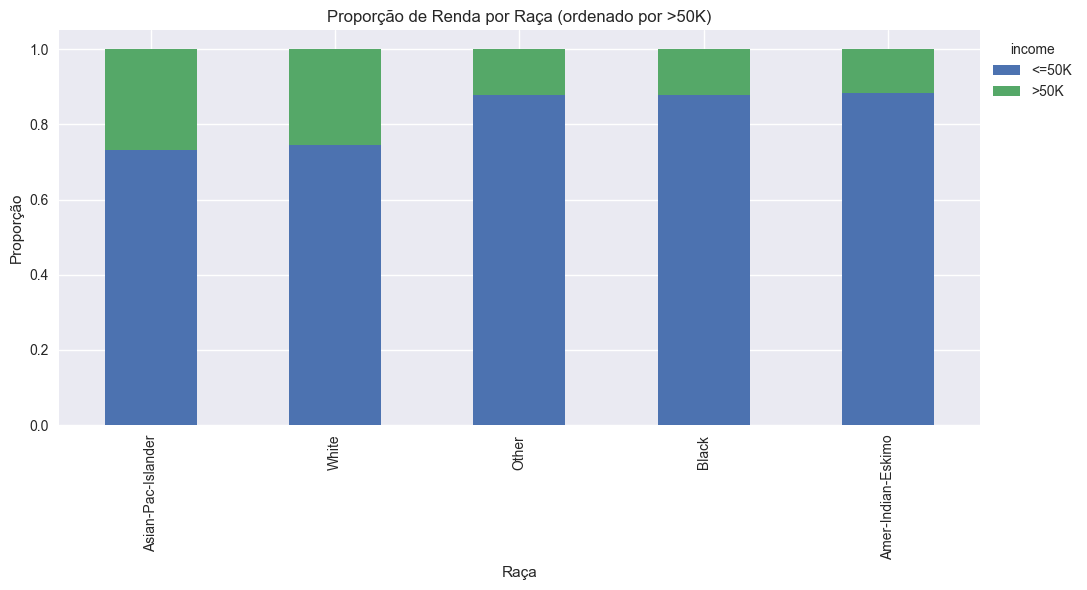 Figura: Proporção das classes de renda por raça.
Figura: Proporção das classes de renda por raça.
O gráfico revela que as proporções de indivíduos com renda superior a $50K variam entre os grupos raciais, sendo mais elevadas para Asian-Pac-Islander e White. Já as categorias Other, Black e Amer-Indian-Eskimo apresentam proporções menores, indicando possíveis desigualdades que merecem atenção em análises de justiça e explicabilidade.
Interação entre Variáveis Sensíveis: Gênero e Educação
Explorar a interação entre variáveis sensíveis, como gênero e educação, permite identificar padrões mais complexos de desigualdade e possíveis pontos de atenção para explicabilidade e fairness.
# Interação entre gênero e educação na renda
plt.figure(figsize=(12, 6))
sns.barplot(x='education', y='income_num', hue='sex', data=df, errorbar=None)
plt.title('Proporção de Renda >$50K por Nível Educacional e Gênero')
plt.xlabel('Nível Educacional')
plt.ylabel('Proporção de >$50K')
plt.xticks(rotation=45)
plt.tight_layout()
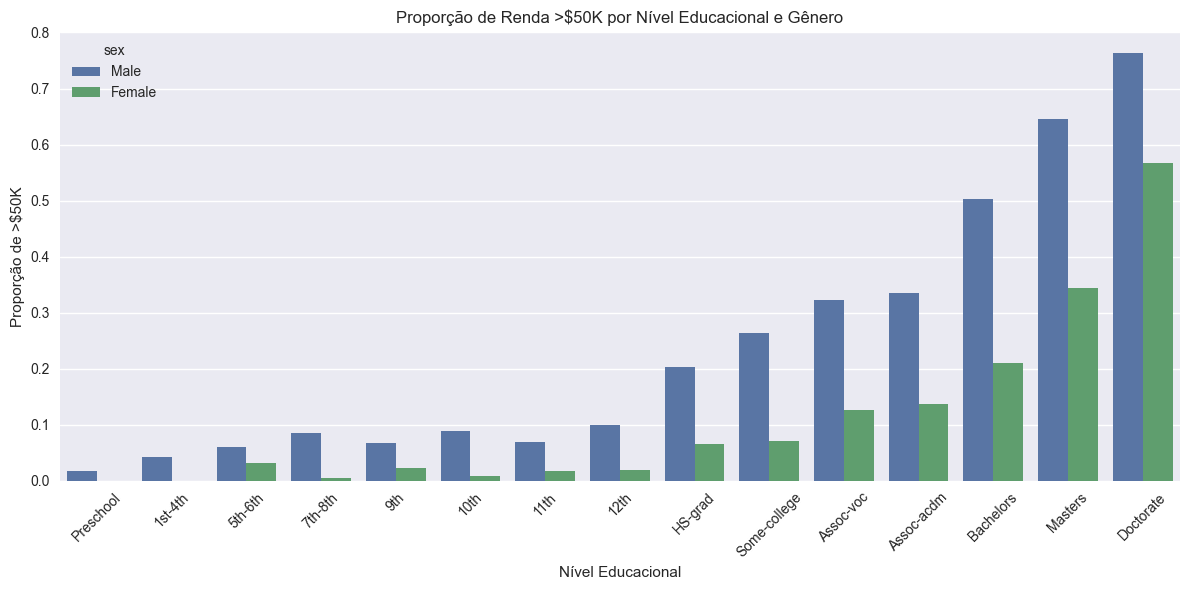 Figura: Proporção de indivíduos com renda >$50K por nível educacional e gênero.
Figura: Proporção de indivíduos com renda >$50K por nível educacional e gênero.
O gráfico evidencia que o aumento do nível educacional está associado a uma maior proporção de indivíduos com renda superior a $50K, tanto para homens quanto para mulheres. No entanto, observa-se que, em todos os níveis, a proporção é consistentemente maior entre os homens, e essa diferença se mantém mesmo nos níveis mais altos de escolaridade. Essa análise é fundamental para o objetivo do estudo, pois demonstra que, mesmo controlando para educação, diferenças de renda por gênero persistem. Isso reforça a importância de abordagens explicáveis e justas na modelagem, permitindo identificar e mitigar potenciais vieses de gênero em decisões automatizadas.
Distribuição de Horas Trabalhadas por Faixa de Renda
A quantidade de horas trabalhadas pode influenciar diretamente a renda, mas também pode refletir diferenças de acesso a oportunidades e condições de trabalho.
# Distribuição de horas trabalhadas por faixa de renda
plt.figure(figsize=(8, 6))
sns.violinplot(x='income', y='hours-per-week', data=df, cut=0)
plt.title('Distribuição de Horas Trabalhadas por Faixa de Renda')
plt.xlabel('Renda')
plt.ylabel('Horas por Semana')
plt.ylim(0, 100) # Limite superior aumentado para melhor visualização
plt.tight_layout()
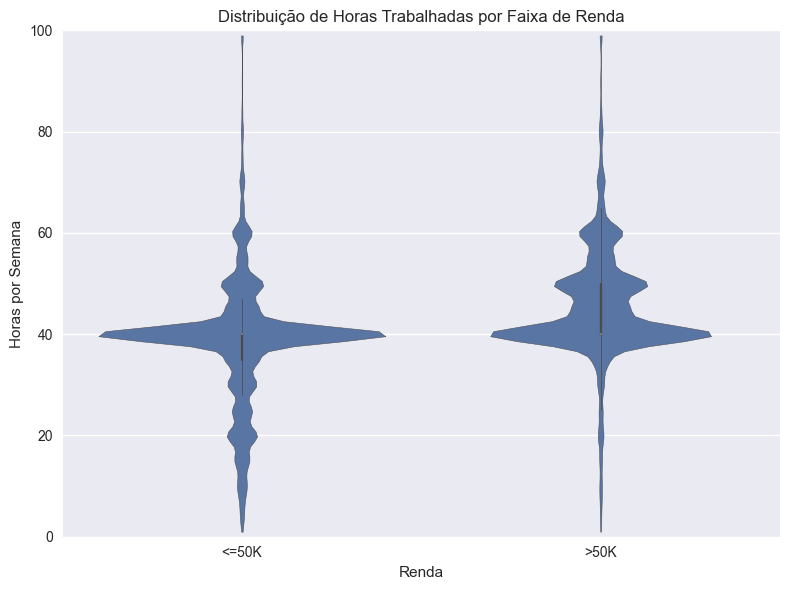 Figura: Distribuição de horas trabalhadas por faixa de renda (violin plot).
Figura: Distribuição de horas trabalhadas por faixa de renda (violin plot).
O violin plot evidencia que, embora a mediana e a distribuição de horas trabalhadas sejam maiores para quem ganha mais de $50K, existe uma grande sobreposição entre os grupos. Isso sugere que, apesar de trabalhar mais horas estar associado a maiores rendas, outros fatores também desempenham papel importante na determinação da renda.
Mapa de Correlação Entre Variáveis Numéricas
Visualizar a correlação entre variáveis numéricas auxilia na identificação de relações lineares e possíveis colinearidades, aspectos importantes para a modelagem e explicabilidade.
# Mapa de correlação entre variáveis numéricas
plt.figure(figsize=(8, 6))
numeric_cols = ['age', 'education-num', 'hours-per-week', 'capital-gain', 'capital-loss']
correlation_matrix = df[numeric_cols].corr()
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', center=0)
plt.title('Matriz de Correlação entre Variáveis Numéricas')
plt.tight_layout()
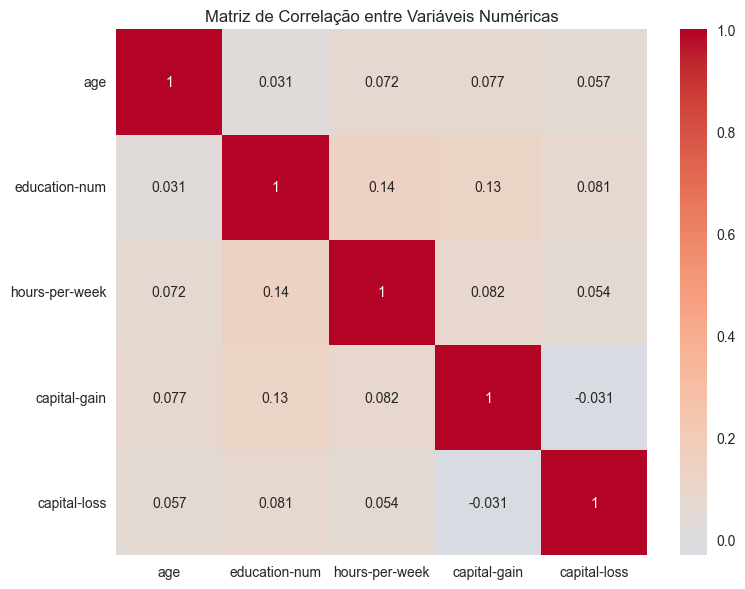 Figura: Mapa de correlação entre variáveis numéricas do dataset.
Figura: Mapa de correlação entre variáveis numéricas do dataset.
O mapa de correlação mostra que as variáveis numéricas do dataset apresentam baixas correlações entre si, sugerindo relativa independência linear entre idade, anos de educação, horas trabalhadas, capital ganho e capital perdido. Esse padrão é positivo para a modelagem, pois reduz o risco de colinearidade e facilita a interpretação dos efeitos individuais de cada variável.
Análise de País de Origem e Renda
A variável país de origem pode revelar diferenças de renda entre nativos e imigrantes, sendo relevante para políticas públicas e fairness em modelos preditivos.
# Proporção de renda por país de origem (exibindo apenas os 10 principais, sem valores ausentes)
df_country = df[df['native-country'] != '?']
top_countries = df_country['native-country'].value_counts().index[:10]
country_income = pd.crosstab(df_country[df_country['native-country'].isin(top_countries)]['native-country'],
df_country['income'], normalize='index')
country_income = country_income.sort_values(by='>50K', ascending=False)
country_income.plot(kind='bar', stacked=True, figsize=(12, 6))
plt.title('Proporção de Renda por País de Origem (Top 10, ordenado por >50K, sem valores ausentes)')
plt.xlabel('País de Origem')
plt.ylabel('Proporção')
plt.tight_layout()
plt.legend(title='income', loc='upper left', bbox_to_anchor=(1,1))
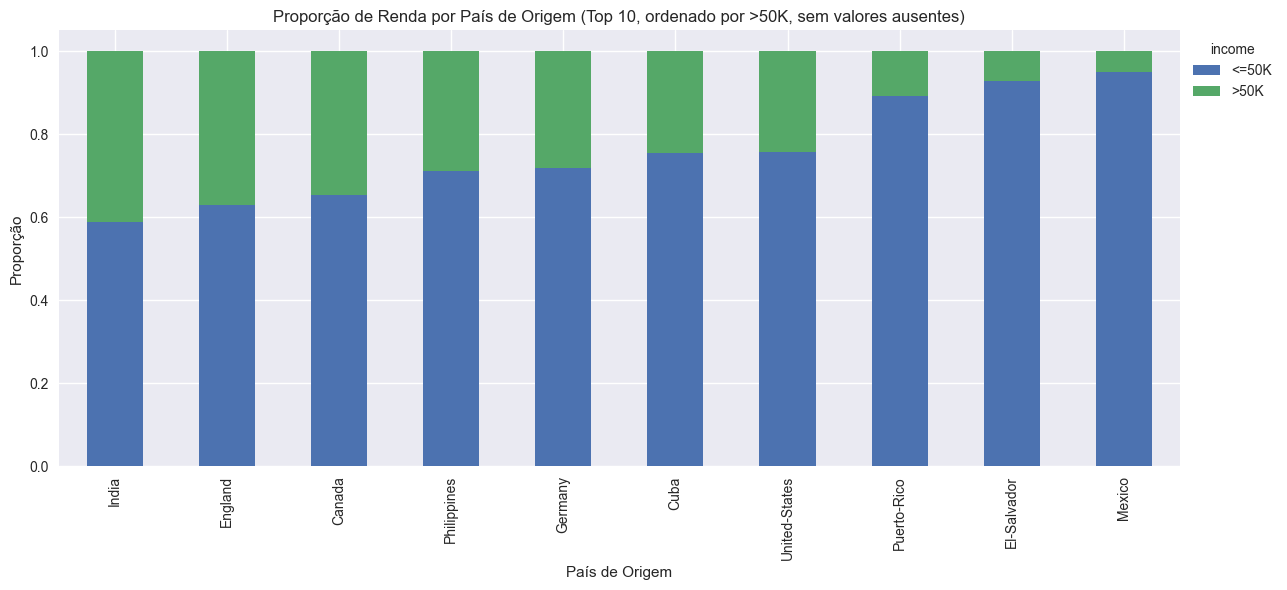 Figura: Proporção das classes de renda por país de origem (10 principais, sem valores ausentes).
Figura: Proporção das classes de renda por país de origem (10 principais, sem valores ausentes).
O gráfico revela diferenças marcantes na proporção de indivíduos com renda superior a $50K entre os principais países de origem. Enquanto Índia e Canadá apresentam as maiores proporções, países latino-americanos como México e El Salvador concentram a maior parte dos indivíduos na faixa de renda mais baixa. Essas diferenças podem refletir barreiras estruturais e desigualdades de acesso ao mercado de trabalho, aspectos relevantes para a análise de fairness e explicabilidade em modelos preditivos.
Comentários